Construction of a triangle given a base and base angle and the difference of other two sides
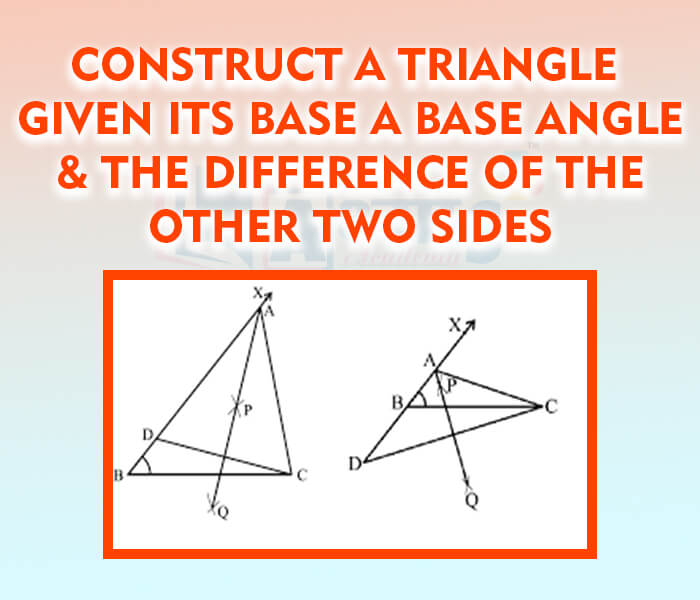
Construction of a triangle given a base and base angle and the difference of other two sides
Construction of a triangle given a base and base angle and the difference of other two sides : In order to contruct a triangle when its base, difference of the other two sides and one of the base angles are given, we follow the following steps:
Steps of Contruction: Obtain the base, base angle and the difference of two other sides. Let BC be the base, be the base angle and x be the difference of the other two sides AB and AC of
.. There can be two cases
Case I: AB > AC i.e., x =AB - AC
STEP I Draw the base BC of given length. STEP II Draw STEP III AS AB > AC , then cut off segment BD = AB - AC from ray BX STEP IV . Join DC |  |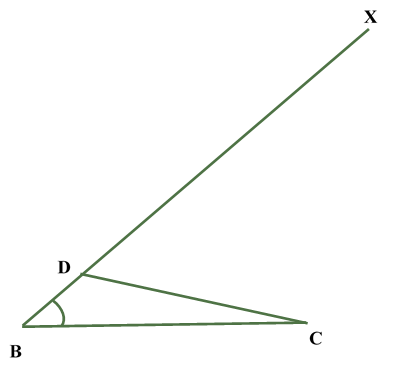
| STEP V: From point C taking radius more than half of CD Draw arc on both side of CD. |  |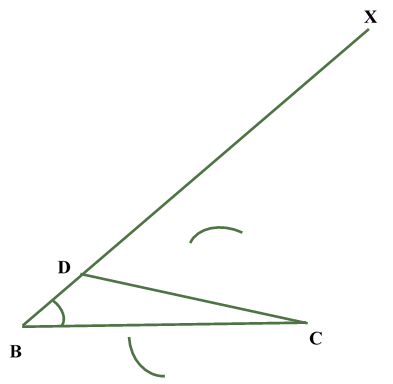
| STEP VI : From point D taking same radius as in step V Draw arc on both side of CD to intersect the arcs drawn in step V at point P and Q. |  |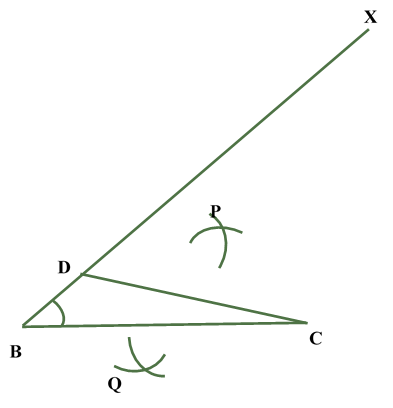
| STEP VII : Join PQ . This is the perpendicular bisector of CD meeting BX at A. |  |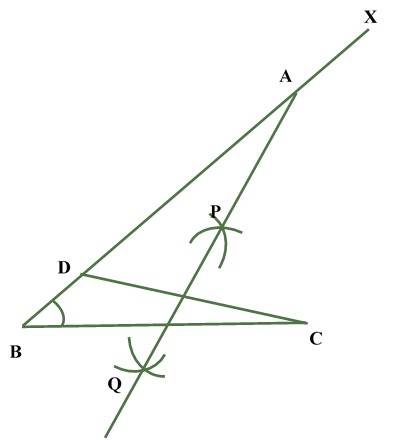
| STEP VIII Join AC to obtain the required triangle ABC. |  |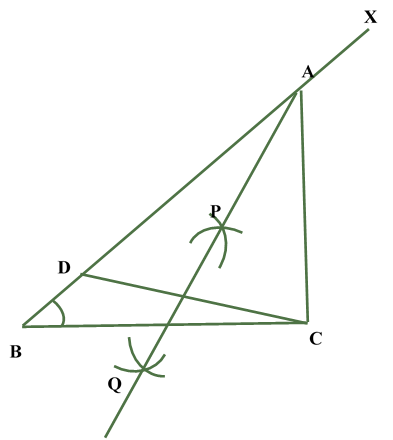
Case II: AC > AB i.e., x =AC - AB
STEP I Draw the base BC of given length. STEP II Draw STEP III As AC > AB ,extend XB to D such that BD = AC - AB STEP IV . Join DC |  |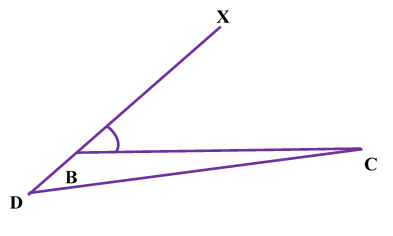
| STEP V: From point C taking radius more than half of CD Draw arc on both side of CD. |  |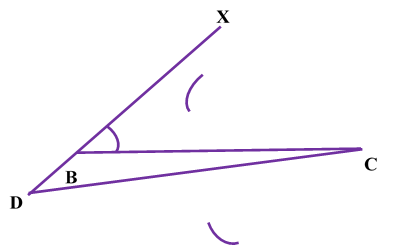
| STEP VI : From point D taking same radius as in step V Draw arc on both side of CD to intersect the arcs drawn in step V at point P and Q. |  |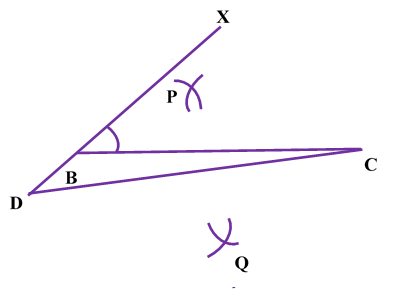
| STEP VII : Join PQ . This is the perpendicular bisector of CD meeting BX at A. |  |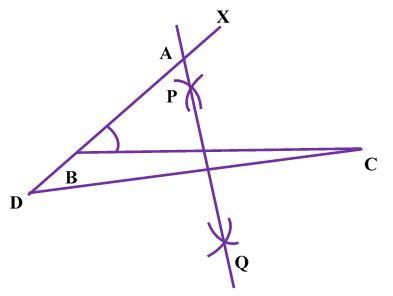
| STEP VIII Join AC to obtain the required triangle ABC. |  |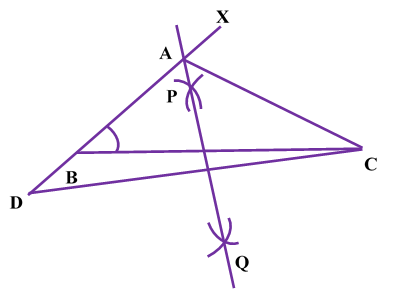
Justification: Let us now see how do we get the required triangle. Since A lies on the perpendicular bisector of DC.
AD = AC
So, BD = AD - AB = AC - AB
Example : Construct a triangle ABC in which base AB = 5 cm, and AC - BC = 2.5 cm.
SOLUTION In order to construct the triangle ABC, we follow the following steps:
Steps of Construction:
STEP I Draw base AB = 5 cm
STEP II Draw
STEP III From ray AX, cut off line segment AD = 2.5 cm(=AC-BC)
STEP IV Join BD.
STEP V Draw the perpendicular bisector of BD which cuts AX at C.
STEP VI Join BC to obtain the required triangle ABC.
Justification: Since C lies on the perpendicular bisector of DB. THerefore,
CD = CB
Now, AD = 2.5 cm
AC - CD = 2.5 cm
AC - BC = 2.5 cm
Hence, is the required triangle.
Students / Parents Reviews [10]
My experience with Abhyas is very good. I have learnt many things here like vedic maths and reasoning also. Teachers here first take our doubts and then there are assignments to verify our weak points.
Shivam Rana
7thAbout Abhyas metholodology the teachers are very nice and hardworking toward students.The Centre Head Mrs Anu Sethi is also a brilliant teacher.Abhyas has taught me how to overcome problems and has always taken my doubts and suppoeted me.
Shreya Shrivastava
8thIt was a good experience with Abhyas Academy. I even faced problems in starting but slowly and steadily overcomed. Especially reasoning classes helped me a lot.
Cheshta
10thA marvelous experience with Abhyas. I am glad to share that my ward has achieved more than enough at the Ambala ABHYAS centre. Years have passed on and more and more he has gained. May the centre flourish and develop day by day by the grace of God.
Archit Segal
7thOne of the best institutes to develope a child interest in studies.Provides SST and English knowledge also unlike other institutes. Teachers are co operative and friendly online tests andPPT develope practical knowledge also.
Aman Kumar Shrivastava
10thI have spent a wonderful time in Abhyas academy. It has made my reasoning more apt, English more stronger and Maths an interesting subject for me. It has given me a habbit of self studying
Yatharthi Sharma
10thIt was good as the experience because as we had come here we had been improved in a such envirnment created here.Extra is taught which is beneficial for future.
Eshan Arora
8thMy experience with Abhyas academy is very good. I did not think that my every subject coming here will be so strong. The main thing is that the online tests had made me learn here more things.
Hiya Gupta
8thMy experience was very good with Abhyas academy. I am studying here from 6th class and I am satisfied by its results in my life. I improved a lot here ahead of school syllabus.
Ayan Ghosh
8thBeing a parent, I saw my daughter improvement in her studies by seeing a good result in all day to day compititive exam TMO, NSO, IEO etc and as well as studies. I have got a fruitful result from my daughter.
